2023.09.03

【Pandas】時系列のサンプルデータを作成する【Python】

MAX

時系列でないデータについては、sklearnやseaborn経由などで色々なサンプルデータを簡単に取得することができる（そして分析や機械学習のテストにも十分に使える）。

一方、時系列のサンプルデータはほとんどない。

政府統計やFX、株価関連のデータなどを取得すれば、時系列データを取得できるが、はっきりとした周期生などがない。

トレンドを持つデータなどを作成したい場合、工夫すれば自分で作成することもできる。

Contents

正規分布に基づくランダムなデータ
- 値が1列のデータ
- 値が複数列のデータ
単一の周期性を持つデータ
- サインカーブにノイズを加えたデータ
複数周期のsin波を足し合わせたデータ
まとめ

正規分布に基づくランダムなデータ

numpyのrandom.randnを使うことで、正規分布に基づくデータをランダムに生成することができる。

時系列データで何か試したい時に、周期性のあるデータとの対比として使用するなどが考えられる。

値が1列のデータ

1import numpy as np
2import pandas as pd
3import maptlotlib.pyplot as plt
4import seaborn as sns
5
6# 正規分布に基づくデータを生成
7n_points = 1000
8# ランダムシードを固定
9np.random.seed(42)
10random_data = np.random.randn(n_points)
11# 日付インデックスを生成
12date_index = pd.date_range(start="2020-4-1", periods=n_points, freq="D")
13df = pd.DataFrame(data=random_data, index=date_index, columns=["value"])
14print(df.shape)
15# (1000, 1)
16print(df.head())
17#             value
18# 2020-04-01   0.50
19# 2020-04-02  -0.14
20# 2020-04-03   0.65
21# 2020-04-04   1.52
22# 2020-04-05  -0.23

グラフは以下のようになる

1# プロットすると、完全にランダムな動きだと言うのがわかる
2plt.figure(figsize=(8, 4.5), facecolor="w")
3sns.lineplot(data=df)
4title = "random_noise_data"
5plt.title(title)
6plt.tight_layout()
7plt.show()

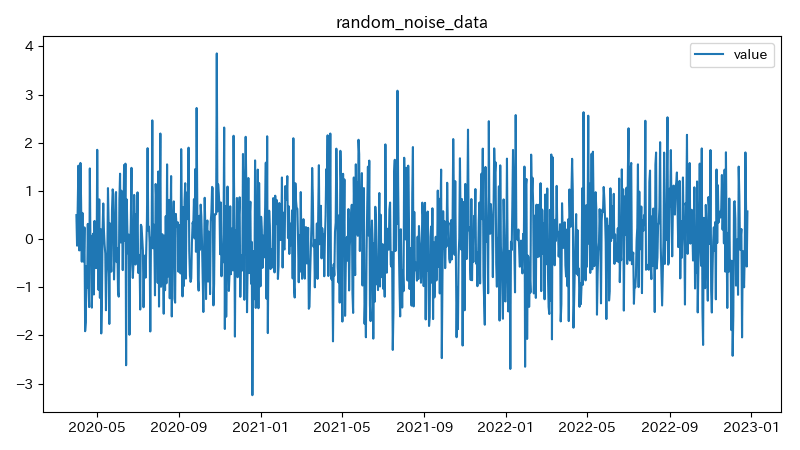
正規分布に基づく乱数なので、周期性は全くない。

値が複数列のデータ

DataFrame作成時に少し注意が必要だが、それ以外は1列の値を作成する時と同じ。

1# 正規分布に基づくデータを生成
2n_points = 1000
3# ランダムシードを固定
4np.random.seed(42)
5random_data1 = np.random.randn(n_points)
6random_data2 = np.random.randn(n_points)
7# 日付インデックスを生成
8date_index = pd.date_range(start="2020-4-1", periods=n_points, freq="D")
9df = pd.DataFrame(data=np.array([random_data1, random_data2]).T, index=date_index, columns=["value1", "value2"])
10print(df.shape)
11# (1000, 2)
12print(df.head())
13#             value1  value2
14# 2020-04-01    0.50    1.40
15# 2020-04-02   -0.14    0.92
16# 2020-04-03    0.65    0.06
17# 2020-04-04    1.52   -0.65
18# 2020-04-05   -0.23    0.70

単一の周期性を持つデータ

サインカーブにノイズを加えたデータ

周期性を持つデータとしてsin波やcos波がある。これをベースに、ノイズを適度に加えることで、周期性を持つデータを作成できる。

1import numpy as np
2import pandas as pd
3import matplotlib.pyplot as plt
4# ランダムシードを固定
5np.random.seed(42)
6
7# 時間データを生成
8n_points = 1000
9t = np.linspace(0, 4 * np.pi, n_points)  # 0から4πまで
10
11# サイン波とコサイン波を生成
12sin_wave = np.sin(t)
13cos_wave = np.cos(t)
14
15# ランダムノイズを加える
16noise_level = 0.2
17sin_wave_noisy = sin_wave + noise_level * np.random.randn(n_points)
18cos_wave_noisy = cos_wave + noise_level * np.random.randn(n_points)
19
20# DataFrame作成
21date_rng = pd.date_range(start='2022-01-01', periods=n_points, freq='D')
22df = pd.DataFrame({
23    'time': t,
24    'sin_wave': sin_wave_noisy,
25    'cos_wave': cos_wave_noisy
26}, index=date_rng)
27print(df.shape)
28# (1000, 3)
29print(df.head())
30#             time  sin_wave  cos_wave
31# 2022-01-01  0.00      0.10      1.28
32# 2022-01-02  0.01     -0.02      1.18
33# 2022-01-03  0.03      0.15      1.01
34# 2022-01-04  0.04      0.34      0.87
35# 2022-01-05  0.05      0.00      1.14

np.linspaceでtの範囲を0〜4πに指定しているが、これは適当である。作成したいデータに合わせて範囲やデータポイントを設定すればいい。

グラフは以下のようになる。

1# プロット
2plt.figure(figsize=(8, 4.5))
3plt.plot(df.index, df['sin_wave'], label='Noisy Sin Wave')
4plt.plot(df.index, df['cos_wave'], label='Noisy Cos Wave')
5plt.legend()
6title = "noisy_sin_cos_wave"
7plt.title(title)
8plt.show()
9

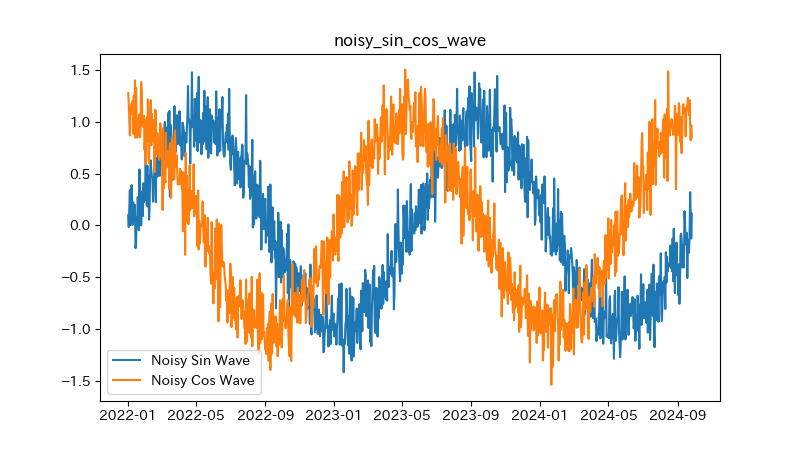
sinカーブ、cosカーブにノイズが加わっているのが分かる。

これだとまだ単純すぎるという場合は、次の複数周期の波を組み合わせる方法もある。

複数周期のsin波を足し合わせたデータ

単一の周期のsin波だけでなく、色々な周期のsin波を足し合わせてデータを作成する。

勿論、ランダムなノイズも加える。

フーリエ逆変換のようなイメージかもしれない。

以下の例では、1分足のデータに対し、4時間、1日、1週間周期のsin波を作成し、足し合わせている。

1import numpy as np
2import pandas as pd
3import matplotlib.pyplot as plt
4# ランダムシードを固定
5np.random.seed(42)
6
7# 1分足のデータを一日分（24 * 60ポイント）作る
8n_points = 24 * 60  
9t = np.linspace(0, 2 * np.pi, n_points)
10
11# 6時間周期、24時間周期、1週間周期の波を生成
12six_hour_wave = np.sin(4 * t)
13one_day_wave = np.sin(t)
14one_week_wave = np.sin(t / 7)
15
16# ランダムノイズを加える
17noise_level = 0.05
18six_hour_wave_noisy = six_hour_wave + noise_level * np.random.randn(n_points)
19one_day_wave_noisy = one_day_wave + noise_level * np.random.randn(n_points)
20one_week_wave_noisy = one_week_wave + noise_level * np.random.randn(n_points)
21
22# 全て足し合わせる
23total_wave = six_hour_wave_noisy + one_day_wave_noisy + one_week_wave_noisy
24
25# DataFrameを作成
26date_rng = pd.date_range(start='2022-01-01', periods=n_points, freq='T')  # 1分足なので'T'を使う
27df = pd.DataFrame({
28    'time': t,
29    'six_hour_wave': six_hour_wave_noisy,
30    'one_day_wave': one_day_wave_noisy,
31    'one_week_wave': one_week_wave_noisy,
32    'total_wave': total_wave
33}, index=date_rng)
34print(df.shape)
35# (1440, 5)
36print(df.head())
37#                      time  six_hour_wave  one_day_wave  one_week_wave  total_wave
38# 2022-01-01 00:00:00  0.00           0.02          0.03          -0.11       -0.05
39# 2022-01-01 00:01:00  0.00           0.01          0.06          -0.11       -0.03
40# 2022-01-01 00:02:00  0.01           0.07          0.02          -0.03        0.06
41# 2022-01-01 00:03:00  0.01           0.13         -0.05           0.02        0.10
42# 2022-01-01 00:04:00  0.02           0.06          0.04          -0.13       -0.04

グラフは以下のようになる。

1# プロットする。6時間の周期がありつつ、１週間の周期があるので下降気味になっているのが分かる
2plt.figure(figsize=(8, 4.5))
3sns.lineplot(data=df, x=df.index, y=df['total_wave'], label='Total Wave')
4plt.legend()
5title = "total_sin_6h_1d_1w"
6plt.title(title)
7plt.show()

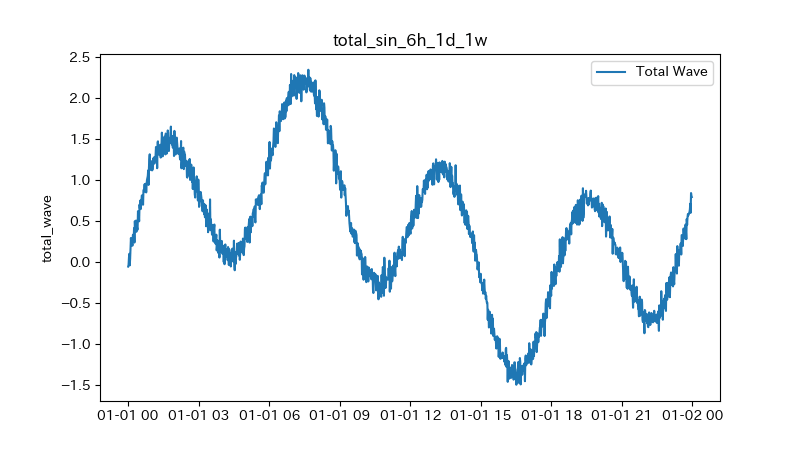
6時間のsinの周期がありつつ、全体として、上昇トレンド、下降トレンドがある。

１分足のデータを1ヶ月分作成する例

np.linspace()で指定する範囲が重要。

以下の例では1日に2πをベースとして、30日分で0〜60πをデータ作成範囲としている。

1import numpy as np
2import pandas as pd
3import matplotlib.pyplot as plt
4# ランダムシードを固定
5np.random.seed(42)
6
7# 1分足のデータを一日分（24 * 60ポイント）作る
8n_dates = 30
9n_points = n_dates * 24 * 60
10t = np.linspace(0, 2 * np.pi * n_dates, n_points)
11
12# 6時間周期、24時間周期、1週間周期の波を生成
13six_hour_wave = np.sin(4 * t / n_dates)
14one_day_wave = np.sin(t / n_dates)
15one_week_wave = np.sin(t / (n_dates * 7))
16
17# ランダムノイズを加える
18noise_level = 0.05
19six_hour_wave_noisy = six_hour_wave + noise_level * np.random.randn(n_points)
20one_day_wave_noisy = one_day_wave + noise_level * np.random.randn(n_points)
21one_week_wave_noisy = one_week_wave + noise_level * np.random.randn(n_points)
22
23# 全て足し合わせる
24total_wave = six_hour_wave_noisy + one_day_wave_noisy + one_week_wave_noisy
25
26# DataFrameを作成
27date_rng = pd.date_range(start='2020-04-15', periods=n_points, freq='T')  # 1分足なので'T'を使う
28df = pd.DataFrame({
29    'time': t,
30    'six_hour_wave': six_hour_wave_noisy,
31    'one_day_wave': one_day_wave_noisy,
32    'one_week_wave': one_week_wave_noisy,
33    'total_wave': total_wave
34}, index=date_rng)
35print(df.shape)
36df.head()

周期はもっと細かく調整したほうが良いかもしれない。

まとめ

1import numpy as np
2import pandas as pd
3import maptlotlib.pyplot as plt
4import seaborn as sns
5# -------------------------------------------------
6# 正規分布に基づくデータ
7# -------------------------------------------------
8n_points = 1000
9# ランダムシードを固定
10np.random.seed(42)
11random_data = np.random.randn(n_points)
12# 日付インデックスを生成
13date_index = pd.date_range(start="2020-4-1", periods=n_points, freq="D")
14df = pd.DataFrame(data=random_data, index=date_index, columns=["value"])
15
16# -------------------------------------------------
17# sin, cosカーブにノイズを加えたデータ
18# -------------------------------------------------
19# ランダムシードを固定
20np.random.seed(42)
21# 時間データを生成
22n_points = 1000
23t = np.linspace(0, 4 * np.pi, n_points)  # 0から4πまで
24# サイン波とコサイン波を生成
25sin_wave = np.sin(t)
26cos_wave = np.cos(t)
27# ランダムノイズを加える
28noise_level = 0.2
29sin_wave_noisy = sin_wave + noise_level * np.random.randn(n_points)
30cos_wave_noisy = cos_wave + noise_level * np.random.randn(n_points)
31# DataFrame作成
32date_rng = pd.date_range(start='2022-01-01', periods=n_points, freq='D')
33df = pd.DataFrame({
34    'time': t,
35    'sin_wave': sin_wave_noisy,
36    'cos_wave': cos_wave_noisy
37}, index=date_rng)
38
39# -------------------------------------------------
40# 複数周期のsin波を足し合わせたデータ
41# -------------------------------------------------
42# ランダムシードを固定
43np.random.seed(42)
44# 1分足のデータを一日分（24 * 60ポイント）作る
45n_points = 24 * 60  
46t = np.linspace(0, 2 * np.pi, n_points)
47# 6時間周期、24時間周期、1週間周期の波を生成
48six_hour_wave = np.sin(4 * t)
49one_day_wave = np.sin(t)
50one_week_wave = np.sin(t / 7)
51# ランダムノイズを加える
52noise_level = 0.05
53six_hour_wave_noisy = six_hour_wave + noise_level * np.random.randn(n_points)
54one_day_wave_noisy = one_day_wave + noise_level * np.random.randn(n_points)
55one_week_wave_noisy = one_week_wave + noise_level * np.random.randn(n_points)
56# 全て足し合わせる
57total_wave = six_hour_wave_noisy + one_day_wave_noisy + one_week_wave_noisy
58# DataFrameを作成
59date_rng = pd.date_range(start='2022-01-01', periods=n_points, freq='T')  # 1分足なので'T'を使う
60df = pd.DataFrame({
61    'time': t,
62    'six_hour_wave': six_hour_wave_noisy,
63    'one_day_wave': one_day_wave_noisy,
64    'one_week_wave': one_week_wave_noisy,
65    'total_wave': total_wave
66}, index=date_rng)

#pandas

ABOUT ME

【Pandas】時系列のサンプルデータを作成する【Python】

正規分布に基づくランダムなデータ

値が1列のデータ

値が複数列のデータ

単一の周期性を持つデータ

サインカーブにノイズを加えたデータ

複数周期のsin波を足し合わせたデータ

１分足のデータを1ヶ月分作成する例

まとめ

【Pandas】日付インデックスの頻度を判定する

【Pandas】インデックス用の日付を作成する

【Python】【Pandas】文字列が数値かどうかを確認する

【Pandas】DataFrameの列が日付型かどうかを判定する

【Pandas】特定の列名を修正する

【Python】【Pandas】DataFrameやSeriesでのループ処理