【matplotlib】グラフタイトルのサイズと色を変更する【Python】
MAX
MAX999blog
【Python】【scipy】ベータ分布のグラフ作成
MAX
ベータ分布は[0, 1]の区間でαとβの値を色々設定することで、分布の形が変わる。
グラフの作成はscipyのstatsから行える。
ベータ分布に従う乱数生成はscipyのstatsやnumpyから行える。
[0, 1]で分布の形をある程度コントロール可能なので、正規分布などの無限に広がる分布よりも使いやすかったりする。
Contents
スポンサーリンク
ベータ分布のグラフ作成
scipy.statsでベータ分布のグラフを作成することが可能。
乱数を生成するのが目的であっても、確率密度関数の形は確認しておいた方が良いと思う。
n=100ぐらいに分割すれば、滑らかに見える。
scipyのstatsにbetaがあり、pdfが用意されているので、それを使う。
1import numpy as np
2from scipy.stats import beta
3
4# [0, 1]で0.1刻みの値を作成
5x = np.linspace(0, 1, 101)
6# β分布の値作成
7a = 3
8b = 3
9y = beta.pdf(x, a, b)
10# グラフ描画
11plt.figure(figsize=(8, 4.5), facecolor="w")
12plt.plot(x, y, label=f"{a=}, {b=}")
13plt.legend(loc="upper right")
14plt.tight_layout()
15plt.show()
色々なベータ分布の形
αとβの値を変えることで、分布の形を色々と変えられる。
一様分布にしたり、正規分布に近い形にしたり、偏りのある分布にしたりすることが可能。
一様分布（α=1かつβ=1）
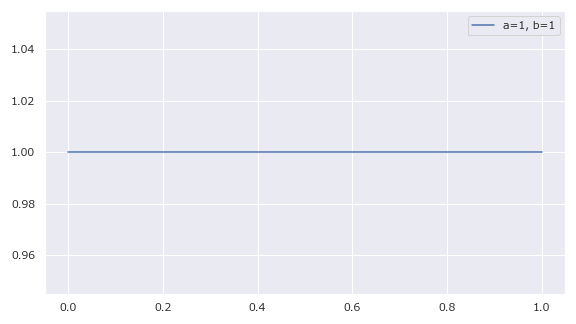
αもβも1にすることで、一様分布の形になる。
1# [0, 1]で0.1刻みの値を作成
2x = np.linspace(0, 1, 101)
3# β分布パラメータ設定
4a, b = 1, 1
5# グラフ描画
6plt.figure(figsize=(8, 4.5), facecolor="w")
7plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
8plt.legend(loc="upper right")
9plt.tight_layout()
10plt.show()
正規分布のような形（α=βかつ3≦α, β≦7）
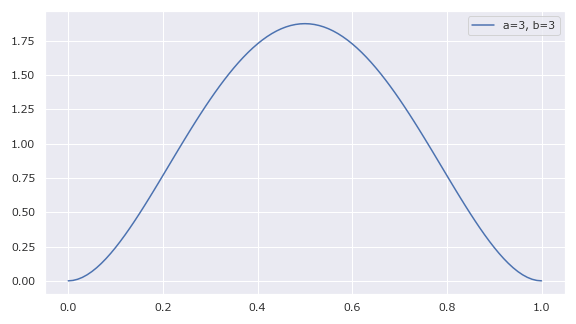
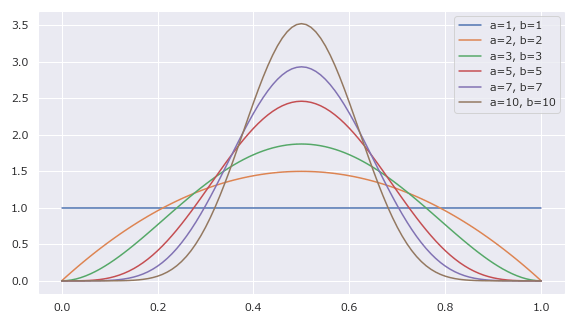
α=βで、αとβが3～7ぐらいにすると、正規分布っぽい形になる。
正規分布だと、裾が無限に広がるが、ベータ分布は区間が[0, 1]なので無限が嫌な時に正規分布の代替的なものとして使える。
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4# β分布パラメータ設定
5params = [(1, 1), (2, 2), (3, 3), (5, 5), (7, 7), (10, 10)]
6# 各パラメータでグラフ描画
7for a, b in params:
8 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
9
10plt.legend(loc="upper right")
11plt.tight_layout()
12plt.show()
α=βかつα, β<1
0付近、1付近で無限大になる。
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4# β分布パラメータ設定
5params = [(0.1, 0.1), (0.5, 0.5), (0.9, 0.9)]
6# 各パラメータでグラフ描画
7for a, b in params:
8 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
9
10plt.legend(loc="upper center")
11plt.tight_layout()
12plt.show()
偏った形（1≦α＜β）（1≦β＜α）
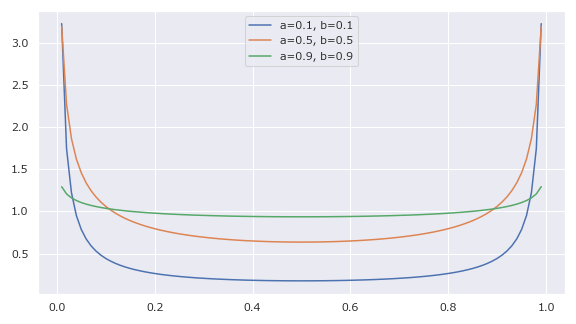
αとβが両方とも1以上なので、有限の値になる。
α≠βにすることで、正規分布を少し偏らせた分布を得ることができる。
1≦α＜β
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4# β分布パラメータ設定
5params = [(1, 5), (1.5, 5), (2.5, 5), (3, 5)]
6# 各パラメータでグラフ描画
7for a, b in params:
8 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
9
10plt.legend(loc="upper right")
11plt.tight_layout()
12plt.show()
1≦β＜α
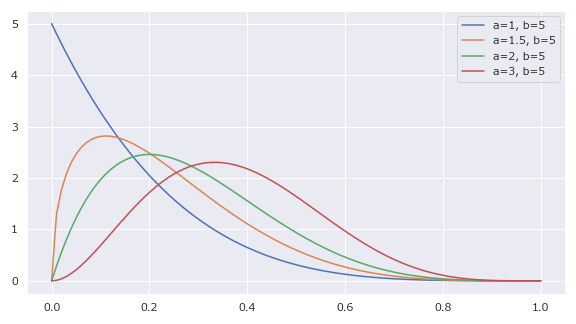
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4# β分布パラメータ設定
5params = [(5, 1), (5, 1.5), (5, 2.5), (5, 3)]
6# 各パラメータでグラフ描画
7for a, b in params:
8 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
9
10plt.legend(loc="upper left")
11plt.tight_layout()
12plt.show()
偏った形（α<1≦β）（β<1≦α）
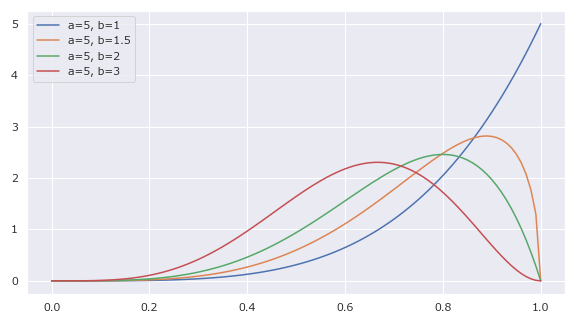
1より小さい方は発散し、1以上の方は収束する。
α<1≦β
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4# β分布パラメータ設定
5params = [(0.1, 1.1), (0.5, 2.5), (0.9, 9)]
6# 各パラメータでグラフ描画
7for a, b in params:
8 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
9
10plt.legend(loc="upper right")
11plt.tight_layout()
12plt.show()
β<1≦α
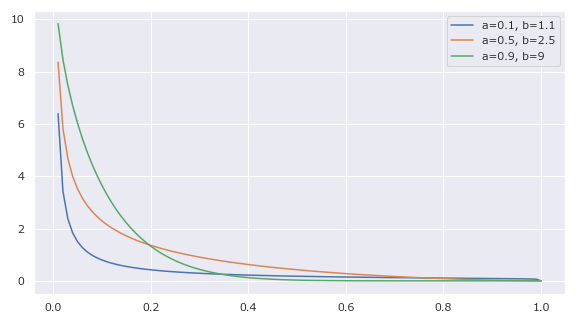
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4params = [(1.1, 0.1), (2.5, 0.5), (9, 0.9)]
5# 各パラメータでグラフ描画
6for a, b in params:
7 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
8
9plt.legend(loc="upper left")
10plt.tight_layout()
11plt.show()
偏った形（α<β<1）（β<α<1）
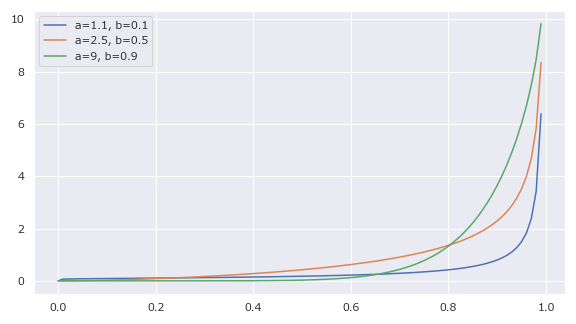
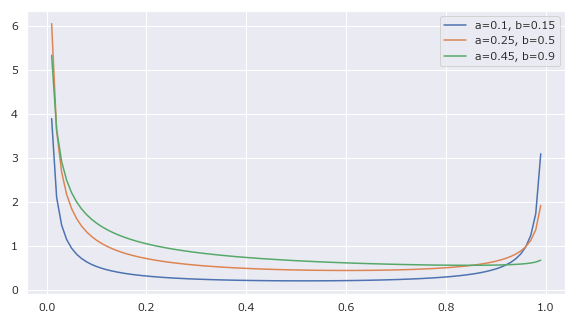
両端共に１より小さいので発散する。
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4params = [(0.1, 0.15), (0.25, 0.5), (0.45, 0.9)]
5# 各パラメータでグラフ描画
6for a, b in params:
7 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
8
9plt.legend(loc="upper right")
10plt.tight_layout()
11plt.show()
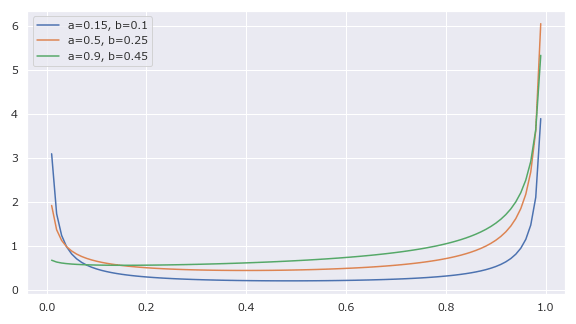
1plt.figure(figsize=(8, 4.5), facecolor="w")
2# [0, 1]で0.1刻みの値を作成
3x = np.linspace(0, 1, 101)
4params = [(0.15, 0.1), (0.5, 0.25), (0.9, 0.45)]
5# 各パラメータでグラフ描画
6for a, b in params:
7 plt.plot(x, beta.pdf(x, a, b), label=f"{a=}, {b=}")
8
9plt.legend(loc="upper left")
10plt.tight_layout()
11plt.show()
まとめ
- パラメータを1以上にすると値は有限になる。
- パラメータを1未満にすると各末端で発散する。
- パラメータの値を調整することで、正規分布に近い形や少し偏った分布を作成することが可能。
スポンサーリンク
ABOUT ME
新卒でSIerに入社し、フリーランスになってWEB系へ転向。
その後AIの世界へ足を踏み入れ、正社員に戻る。 テーブルデータの分析がメイン。
その後AIの世界へ足を踏み入れ、正社員に戻る。 テーブルデータの分析がメイン。
